Cantor's pairing / unpairing for non diagonal unordered pairs

1. Intention

This article is a quick follow up to the previous blog entry about creating a logical index from an unordered, non diagonal pair, based upon the Cantor's pairing algorithm.

2. Cantor's pairing

Cantor's pairing function \(C(x,y)\)associates a unique integer number \(n\) for any given pair of positive integers \((x,y)\)following the formula:

$$C(x,y) = \frac{x^2 + 3x +2xy+y+y^2}{2}$$

The advantage of that function, compared to using a simple bit allocation and bit shifting, is that it doesn't require a size or number of elements to work with. This is pretty practical to be used with algorithms in 2D or 3D, where a hashing function is required to store spatial data in dictionaries of hash sets.

The way the function associates values is by filling the positive side of the 2D plane in a diagonal pattern, which is pretty neat to see:

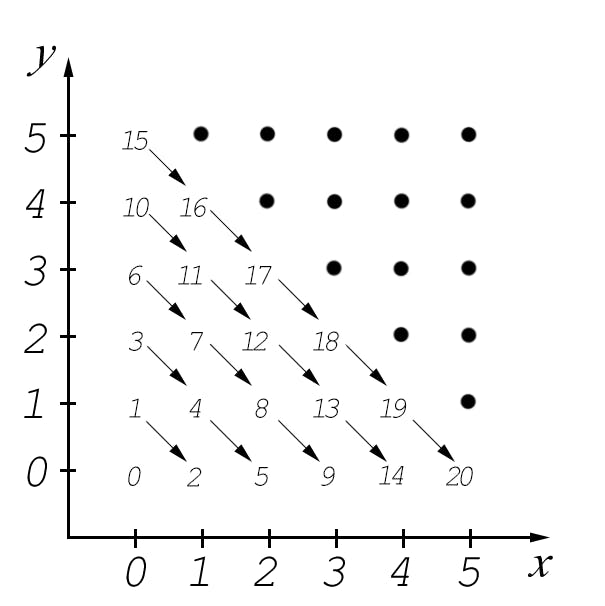
3. Adaptation to unordered non diagonal pairs

Below is the same diagram we used to illustrate the pairs resulting from \(n=5\):

And below are Cantor values, using the same axis representation:

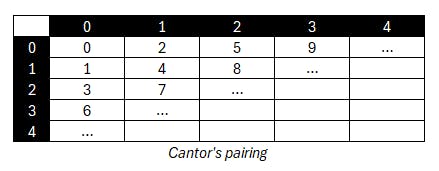
Looking at the two diagram above, it becomes obvious that we can mirror the Cantor pairing values along the \(x\) axis, in order to get values that perfectly fit our pairs. It becomes also obvious that supporting diagonal pairs would come for free as well, which is a neat side effect of using this method.

After mirroring, we simply get:

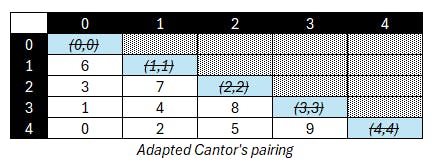
Which leads to the following code:

uint64_t ComputeIndex_Cantor(int n, int x, int y)
{
    uint64_t adjustedY = uint64_t(n) - 1 - y;
    return (uint64_t(x) * x + 3LL * x + 2LL * x * adjustedY + adjustedY + adjustedY * adjustedY) >> 1;
}

4. Unpairing function

Compared to my last blog entry, I won't go into the details of that formula, as literature exists on the subject. Given a Cantor positive index \(z\), we can retrieve the original pair \((x,y)\) the following way:

$$i = \lfloor{\frac{-1+\sqrt{1+8z}}{2}}\rfloor$$

$$ (x,y) = (z-\frac{i(i+1)}{2},\frac{i(i+3)}{2}-z)$$

Which leads to the following code:

void ComputePairFromIndex_Cantor(int n, uint64_t index, int& x, int& y)
{
    int64_t i = int64_t((-1 + ::std::sqrt(1.0 + index * 8.0)) / 2.0);
    x = int(index - i * (1 + i) / 2);
    y = int(i * (3 + i) / 2 - index);
    y = n - 1 - y;
}

5. Closing comments

I had to opportunity to quickly test the performance compared to the previous one based on logical indices, and this approach is a bit slower. I didn't attempt to optimize the code or improve its robustness with very big values of \(n\). so this exercise will be left to the reader.

For people interested with the topic of pairing functions, I suggest looking up the 'Elegant Pairing' function, which is another neat one that has nice properties in terms of increasing neatly in relation to the distance to the origin, which might be useful as well for some 2D/3D algorithms.

See: NKS2006, WolframScience Conference