1. Intention

This article addresses the math and code for \((x,y)\) integer pairs, and their corresponding logical order indices. If the code below resonates with you, this article might be helpful:

int logicalIndex=0;
int n = ...;
for (int x = 0; x < n - 1; ++x) {
    for (int y = x + 1; y < n; ++y) {
        printf("Pair (%d,%d) has an index of %d\n", x, y, logicalIndex);
        logicalIndex++;
    }
}

Pairs can represent a variety of things, but usually the code above would iterate through object pairs, excluding diagonal pairs\((x=y)\). The structure of the typical double for loop also guaranties that \(y>x\), so for example the pair \((2,1)\) isn't valid, and \((1,2)\) should be used instead.

This article will answer two questions:

• How can we directly compute the logicalIndex for a given \((x,y)\) pair?

• How can we compute back \((x,y)\) for a given logicalIndex ?

2. Computing a logical index from a \((x,y)\) pair

First of all, let's look at a visual representation of the problem space:

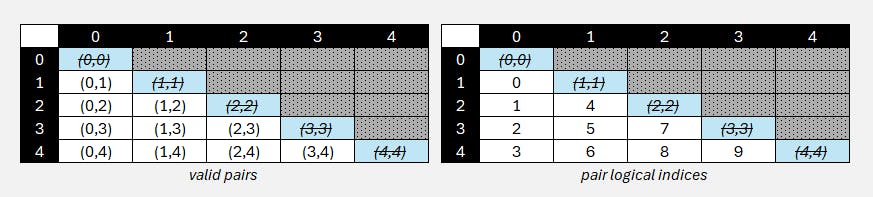
On the left, the table shows \((x,y)\) pairs for \(n=5\), which leads to 10 pairs in total. The valid space where \(y>x \) is the bottom left triangle of the table, invalid diagonal pairs are struck through in the blue cells, and don't contribute to the indices.

On the right, the corresponding logical indices for each pair is described.

The total number of pairs for any given \(n\) can be computed with the following sum function \(S(n)\):

$$S(n)=\sum_{x=0}^{n-2}\sum_{y=x+1}^{n-1}1$$

This first sum is composed of \((n-1) \) terms since \(x\in[0,n-2]\). The inner sum can be directly computed as \(n-1-(x+1)+1\):

$$S(n) = \sum_{x=0}^{n-2}(n-1-(x+1)+1)$$

$$S(n) = \sum_{x=0}^{n-2}(n-x-1)$$

$$(1)\quad S(n)=(n-1)\ +\ (n-2)\quad ...\quad 2 \quad + \quad 1\quad \quad $$

$$(2)\quad S(n) = \quad 1\quad +\quad \ 2\quad ... \quad (n-2)+(n-1)$$

Adding \( (1)+(2)\) term by term, which both have \((n-1)\) terms, we end up with the following:

$$2S(n) = (n-1+1) + (n-2+2) \ ... \ (2+n-2)+(1+n-1) $$

$$2S(n)= n+n \ + \ ... \ + n+n$$

$$\fbox{$\bbox[4pt]{S(n)=\frac{n(n-1)}{2}}$}$$

Having the total loop count is helpful to allocate buffers beforehand to store per-pair data, ideal for cases where dynamic arrays are not acceptable, or when computing a progression ratio is necessary.

Now, how do we get from a \((x,y)\) pair to its corresponding logical index?

We simply split the computation in 2 steps. We start by finding the first logical index for the \(x\) column, which is equivalent to counting all pairs in the prior columns, and subtracting 1 to get a 0-based index.

Second step is trivial, as it's simply adding the number of pairs in the column \(x\), which is simply \(y-x\). This leaves us with:

$$Index = y-x-1+\sum_{i=0}^{x-1}\sum_{j=i+1}^{n-1}1$$

This double sum can be expanded using the same technique as before, which I omit here for simplicity:

$$Index = x(n-1)-\frac{x(x-1)}{2}+y-x-1$$

Expressed in a more computer-friendly way:

$$\fbox{$\bbox[4pt]{Index = \frac{x(2n-x-1)}{2}+y-x-1}$}$$

This finally gives us this first C++ function:

uint64_t ComputeIndex_Logical(int n, int x, int y)
{
    return ((uint64_t(x) * ((2 * n - 1) - x)) >> 1) + y - x - 1;
}

3. Retrieving back a \((x,y)\) pair from its logical index

This one is a little bit more involved. We start from the offset equation and expand it:

$$f(x,y,n)=\frac{x(2n-x-1)}{2}+y-x-1$$

$$f(x,y,n)=\frac{2nx-x^2-x}{2}+x+y-1$$

$$f(x,y,n)=-\frac{x^2}{2}+xn-\frac{3x}{2}+y-1$$

We set the index we want to reverse as \(f\), to make things a bit easier to read, and deduce the value of \(y\):

$$f=f(x,y,n)$$

$$\fbox{$\bbox[4pt]{y = f+\frac{x^2}{2}-nx+\frac{3x}{2}+1}$}$$

This will come handy... once we figure out the value of \(x\).

To find it, we leverage the fact that \(y>x\). By swapping the \(y\) term with the equation just above, we can do an quadratic integer solve for \(x\).

Once the proper root is found, we have to take it as is if it lands perfectly on an integer, but if that's not the case, we need to look for the next integer that still satisfy the inequation \(y>x\).

To simplify this, we can instead solve for \(y >= x + \frac{1}{2}\)which is true as well since we are doing an integer solve, and \(x,y\in{N}\). This leaves us with just one case to deal with which is \(x = \lfloor root \rfloor\). This will become clearer after the solve:

$$f+\frac{x^2}{2}-nx+\frac{3x}{2}+1 \ge x + \frac{1}{2}$$

$$f+\frac{x^2}{2}-nx+\frac{3x}{2}+1-x-\frac{1}{2}\ge0$$

$$\frac{2f}{2}+\frac{x^2}{2}-\frac{2nx}{2}+\frac{3x}{2}+\frac{1}{2}-\frac{2x}{2}\ge0$$

$$2f+{x^2}-2nx+3x+1-2x\ge0$$

$$\fbox{$\bbox[4pt]{{x^2}+x(1-2n)+(2f+1)\ge0}$}$$

The resulting quadratic function is then trivial to solve. If we set the quadratic form as \( f(x) = ax^2+bx+c\) we get the following:

$$a=1$$

$$b=1−2n$$

$$c=2f+1$$

$$Roots=n−\frac{1}{2}±\frac{\sqrt{b^2−4ac}}{2}$$

Setting the discriminant as Δ, we can proceed:

$$Δ = (1-2n)^2-4(2f+1)$$

$$Δ = 4n^2-4n-8f-3$$

$$\fbox{$\bbox[4pt]{Δ = 4(n^2-n-\frac{3}{4}-2f)}$}$$

$$Roots = n-\frac{1}{2}±\frac{\sqrt{4}\sqrt{(n^2-n-\frac{3}{4}-2f)}}{2}$$

$$\fbox{$\bbox[4pt]{Roots = n-\frac{1}{2}±\sqrt{(n^2-n-\frac{3}{4}-2f)}}$}$$

The reason behind factoring by 4 above was not only to simplify the equation, but also attempt to keep the Δ as low as possible to improve floating point precision, which deteriorate for big numbers.

Δ being always positive for any valid input \(n>1\), the quadratic equation will always have two real solutions. The first one, \(r\) will be in the \([0,n-1]\) range, and the other one, \(r'\)always outside, which means it can be ignored completely:

$$\fbox{$\bbox[4pt]{r = n-\frac{1}{2}-\sqrt{(n^2-n-\frac{3}{4}-2f)}}$} $$

$$r' = n-\frac{1}{2}+\sqrt{(n^2-n-\frac{3}{4}-2f)}$$

Let's call the original inequation \(F(x)\), giving us:

$$F(x) = {x^2}+x(1-2n)+(2f+1)\ge0$$

Since the \(x^2\) term is positive, the parabola forms a \(\cup\) shape intersecting the \(y=0\) axis at both roots, leading to \(F(x)\ge0\) for \(x \in [-\infty, r]\) and \(x\in[r',+\infty]\) as well as \(F(x)<0\) for \(x\in ]r, r'[\).

For illustration purpose, below is a plot for\(f(x) = x^2 - 70x + 1000\):

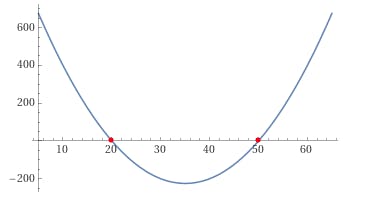
In this plot, the left red dot would be \(r=20\) and the right one \(r'=50\).

As expected \(f(x)\geq 0\) only when \(x\leq r\) and \(x\geq r'\). Since we ignore the right root landing outside of the valid range for \(n\), our solution for \(x\) is the first natural number such as \(x \le r\), fulfilling \(F(x)\ge0\). This is simply a floor operation on the root:

$$\fbox{$\bbox[4pt]{x = \lfloor r \rfloor}$}$$

Once we have \(x\) figured out, finding \(y\) becomes trivial with the earlier formula:

$$\fbox{$\bbox[4pt]{y = f+\frac{x^2}{2}-nx+\frac{3x}{2}+1}$}$$

Which finally gives the full C++ implementation for both pairing and unpairing:

void ComputePairFromIndex_Logical(int n, uint64_t index, int& x, int& y)
{
    uint64_t delta = n * uint64_t(n) - n - 2 * index;
    x = int(n - 0.5 - ::std::sqrt(delta - 3.0 / 4.0));
    y = int(int64_t(x) * (x + 3 - 2 * n) + 2 * (index + 1)) >> 1;
}

uint64_t ComputeIndex_Logical(int n, int x, int y)
{
    return ((uint64_t(x) * ((2 * n - 1) - x)) >> 1) + y - x - 1;
}

3. Warning about precision

This article was made with reasonably large \(n\) in mind. As its value increases, even the double floating point precision will fail to represent the quadratic delta precisely. For example, the long long integer 9867111144222223 cannot be represented accurately with double, which will store 9867111144222224 instead.

For large numbers of \(n\) there are other approaches to find \(x\), like using dichotomy to find the column \(x\) where \(f\) lies withing the first entry \(index (x,x+1)\) and the last entry of the column \(index(x,n-1)\).

Another approach is to refine \(x\) by gradually descending the curve until the first natural number \(x\) verifies \(x^2+x(1-2n)+(2f+1)\ge 0\).

This exercise if left to the reader if the use case described becomes an issue.

Note: This algorighm was tested with values of \(n\) up to 50,000,000.

4. Conclusion & performance

In order to test performance, the following test has been performed. I used \(n \in [0,6000]\), and for each \(n\), the test goes through all possible \((x,y)\)pairs, computing the logical index using the first C++ function, then reversing it back into\((x', y')\), asserting if both pairs don’t turn up the same.

The code has been compiled in release in VS 2022, with floating point precision set to fast, on a 6 cores CPU using a parallel_for (12 concurrent threads).

Benchmark results (the comma is used as a thousands separator):

18,582 ms, total pairs 35,982,002,000, rate : 1,936,390,016 pairs/sec

I will write another blog post using Cantor's pairing function, which looks and performs similarly, but has a interesting and different indexing pattern that could end up more desirable.